Métodos de optimización

Capítulo 1 - Sección 5

---

\[ \def\NN{\mathbb{N}} \def\ZZ{\mathbb{Z}} \def\RR{\mathbb{R}} \def\media{\mathbb{E}} \def\cov{\text{Cov}} \def\prob{\mathbb{P}} \def\calL{\mathcal{L}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calD{\mathcal{D}} \def\calN{\mathcal{N}} \def\aa{{\bf a}} \def\bb{{\bf b}} \def\cc{{\bf c}} \def\dd{{\bf d}} \def\hh{{\bf h}} \def\qq{{\bf q}} \def\xx{{\bf x}} \def\yy{{\bf y}} \def\zz{{\bf z}} \def\uu{{\bf u}} \def\vv{{\bf v}} \def\ww{{\bf w}} \def\XX{{\bf X}} \def\TT{{\bf T}} \def\SS{{\bf S}} \def\bfZ{{\bf Z}} \def\bfg{{\bf g}} \def\bftheta{\boldsymbol{\theta}} \def\bfphi{\boldsymbol{\phi}} \def\bfmu{\boldsymbol{\mu}} \def\bfxi{\boldsymbol{\xi}} \def\bflambda{\boldsymbol{\lambda}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfbeta{\boldsymbol{\beta}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfeta{\boldsymbol{\eta}} \def\bfmu{\boldsymbol{\mu}} \def\bfnu{\boldsymbol{\nu}} \def\bfTheta{\boldsymbol{\Theta}} \def\bfSigma{\boldsymbol{\Sigma}} \def\bfone{\mathbf{1}} \def\bfzero{\mathbf{0}} \def\argmin{\mathop{\mathrm{arg\,min\,}}} \def\argmax{\mathop{\mathrm{arg\,max\,}}} \]

En general, los problemas de optimización que surgen en el área de estadística y machine learning involucran funciones complejas, no lineales y/o de alta dimensión. Como consecuencia, obtener una solución exacta suele ser inalcanzable o innecesario. Esto último sucede, por ejemplo, cuando la solución exacta es costosa computacionalmente.

Aquí es cuando entran en juego los métodos de optimización numérica: algoritmos iterativos que aproximan una solución al problema de optimización. Su objetivo es construir una secuencia de puntos \(\{\xx_t \mid t\in\mathbb{N}_0\}\) que converja al punto óptimo \(\xx^\star\), o lo suficientemente cerca de él.

Los métodos de optimización se definen a partir de las propiedades analíticas de la función objetivo. En esta sección, presentaremos algunos de los métodos fundamentales, construidos bajo distintas suposiciones de diferenciabilidad de \(f\), ya sea utilizando información de primer orden (gradiente), o incorporando información de segundo orden (matriz Hessiana).

Métodos de primer orden

En principio, consideraremos el caso sin restricciones \[ \begin{array}{ll} \text{minimizar } & f(\xx) \end{array} \]

Si \(f\) es una función diferenciable, ya hemos visto que una condición necesaria para que \(\xx^\star\in\RR^p\) resuelve el problema de optimización es que \(\nabla f(\xx^\star)=\mathbf{0}\). Más aún, cuando \(f\) es convexa, la condición también es suficiente (ver Teorema 1 de C1-S4).

Una idea fundamental para construir un algoritmo de optimización es aproximar \(f\) con modelos más simples y manejables. En particular, los métodos de primer orden se basan en la aproximación de Taylor de primer orden alrededor de un punto \(\xx_t\), a saber: \[ f(\xx) \approx f(\xx_{t}) + \nabla f(\xx_{t})^\top(\xx - \xx_{t}). \]

Método de descenso por gradiente

Una propiedad fundamental del vector gradiente \(\nabla f(\xx)\) es que es la dirección de máximo crecimiento de \(f\) a partir del punto \(\xx\). Por lo tanto, una idea básica para minimizar \(f\) es moverse en la dirección opuesta, \(-\nabla f(\xx)\), una determinada distancia, para luego volver a calcular el vector gradiente y repetir el descenso. Esto deriva en el primer algoritmo de optimización que analizaremos.

Método de descenso por gradiente

---

Dado un punto inicial \(\xx_0\in\text{dom}\,f\) y una tasa de aprendizaje \(\eta>0\):

repetir para \(t = 0,1,2,\dots\):

1° Calcular dirección \(-\nabla f(\xx_t)\)

2° Actualizar \(\xx_{t+1} := \xx_t - \eta \nabla f(\xx_t)\).

hasta que el criterio de parada se satisfaga.

---

Figura 1. Interpretación geométrica del método de descenso por gradiente: la dirección de búsqueda es \(-\nabla f(\xx_t)\).

Importante

Como criterio de parada, se puede fijar una cantidad máxima de iteraciones, aunque en general también se utilizan condiciones de convergencia, como que la norma del gradiente sea menor que un umbral prefijado, o que el cambio entre iteraciones sucesivas sea suficientemente pequeño. En fórmulas: \[ \|\nabla f(\xx_t)\|_2<\varepsilon_1\qquad\text{o}\qquad\|\xx_{t}-\xx_{t-1}\|_2<\varepsilon_2. \]

A continuación mostraremos una función en Python que implementa el algoritmo básico de descenso por gradiente, con los siguientes argumentos:

• f: función objetivo.
• grad_f: función gradiente de \(f\).
• x_inicial: punto inicial.
• lr: (learning rate) tasa de aprendizaje \(\eta\).
• max_iter: cantidad máxima de iteraciones.
• tol_grad: tolerancia para norma del gradiente (opcional).
• tol_x: tolerancia para norma de diferencia entre iteraciones (opcional).

La salida es una lista con los puntos obtenidos en las iteraciones (x_iter), y los valores de la función (f_iter).

import numpy as np

def gradient_descent(f, grad_f, x_inicial, lr=0.1, max_iter=100,
                      tol_grad=None, tol_x=None, verbose=True):
   
    x = np.array(x_inicial, dtype=float)
    x_iter = [x.copy()]
    f_iter = [f(x)]

    for t in range(1, max_iter + 1):
      
      grad = grad_f(x)

      # Criterio de parada por norma del gradiente:
      if tol_grad is not None and np.linalg.norm(grad) < tol_grad:
        if verbose:
          print(f"Parada en iteración {t}: |grad_f| < {tol_grad}")
        t = t-1
        break

      x_new = x - lr * grad

      # Criterio de parada por norma de diferencia entre iteraciones:
      if tol_x is not None and np.linalg.norm(x_new - x) < tol_x:
        if verbose:
          print(f"Parada en iteración {t}: |x_t - x_(t+1)| < {tol_x}")
        x = x_new
        x_iter.append(x.copy())
        f_iter.append(f(x))
        break

      x = x_new
      x_iter.append(x.copy())
      f_iter.append(f(x))
  
    if verbose:
      print(f"Iteración final: {t}")
      print(f"Último punto: {x}")
      print(f"Valor de f: {f(x)}")  

    return x_iter, f_iter

Ejemplo 1 Vamos a utilizar el método de descenso por gradiente para aproximarnos al valor mínimo de

\[ f(x,y)=2(x-2)^2+5(y-3)^2, \]

el cual sabemos que ocurre en \((2,3)\) (vértice del paraboloide elíptico). Necesitamos proporcionar el gradiente de \(f\), el cual es \[ \nabla f(x,y)=\left(4(x-2), 10(y-3)\right). \]

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Función y gradiente:
def f(x):
    return 2*(x[0] - 2)**2 + 5*(x[1] - 3)**2

def grad_f(x):
    return np.array([4 * (x[0] - 2), 10 * (x[1] - 3)])

# Parámetros:
x_inicial = (0, 0)
lr = 0.05               
max_iter = 100
tol_grad = 1e-3
tol_x = 1e-3

# Ejecutar GD:
x_iter, f_iter = gradient_descent(f, grad_f, x_inicial, lr, max_iter, tol_grad, tol_x)

Parada en iteración 28: |x_t - x_(t+1)| < 0.001
Iteración final: 28
Último punto: [1.99613144 2.99999999]
Valor de f: 2.9931553533161224e-05

La secuencia de valores obtenidas es:

x_arr = np.array(x_iter)
x_vals = x_arr[:, 0]
y_vals = x_arr[:, 1]
tabla = pd.DataFrame({'x': x_vals, 'y': y_vals})
print(tabla)

           x         y
0   0.000000  0.000000
1   0.400000  1.500000
2   0.720000  2.250000
3   0.976000  2.625000
4   1.180800  2.812500
5   1.344640  2.906250
6   1.475712  2.953125
7   1.580570  2.976562
8   1.664456  2.988281
9   1.731565  2.994141
10  1.785252  2.997070
11  1.828201  2.998535
12  1.862561  2.999268
13  1.890049  2.999634
14  1.912039  2.999817
15  1.929631  2.999908
16  1.943705  2.999954
17  1.954964  2.999977
18  1.963971  2.999989
19  1.971177  2.999994
20  1.976942  2.999997
21  1.981553  2.999999
22  1.985243  2.999999
23  1.988194  3.000000
24  1.990555  3.000000
25  1.992444  3.000000
26  1.993955  3.000000
27  1.995164  3.000000
28  1.996131  3.000000

Por último, vamos a realizar la gráfica en el dominio \(\RR^2\) de la función.

# Grilla para graficar:
x = np.linspace(-0.5, 7, 100)
y = np.linspace(-0.5, 5, 100)
X, Y = np.meshgrid(x, y)
def f_xy(x, y):
    return f(np.array([x, y]))
Z = f_xy(X, Y)


# 📈:
plt.figure(figsize=(10, 6))

# Curvas de nivel:
contours = plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.clabel(contours, inline=True, fontsize=8)

# Ruta de descenso por gradiente:
plt.plot(x_vals, y_vals, marker='o', linestyle='--', color='red', label='Iteraciones')
plt.scatter(2, 3, color='blue', label='Mínimo', zorder=5)

plt.xlabel('x')
plt.ylabel('y')
plt.xlim(-0.2, 4)
plt.ylim(-0.2, 5)
plt.legend(loc='upper right', facecolor='white', framealpha=1)
plt.grid(True)
plt.show()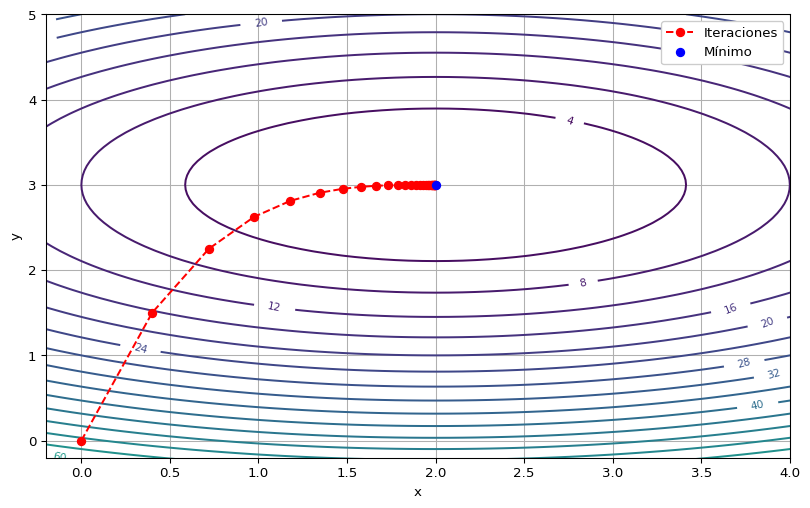

Condición de Lipschitz para el gradiente

Dado que el descenso por gradiente opera considerando la aproximación de primer orden de \(f\), resulta clave preguntarse qué tan rápido deja de ser precisa dicha aproximación. Una respuesta natural surge a partir de la suavidad de \(f\).

Así, una estrategia estándar consiste en imponer una cota sobre qué tan rápido puede cambiar el gradiente de la función al desplazarse ligeramente en cualquier dirección. Como consecuencia, al movernos en dirección de \(-\nabla f(\xx_t)\) desde \(\xx_t\), los nuevos gradientes que encontraremos en el camino permanecerán, en gran medida, alineados con \(\nabla f(\xx_t)\). Esto garantiza que \(-\nabla f(\xx_t)\) seguirá siendo una buena dirección de descenso durante algún tiempo.

Específicamente, requeriremos que el gradiente \(\nabla f(x)\) sea \(L\)-Lipschitz continuo para alguna constante \(L \geq 0\). Esta condición a menudo se llama \(L\)-suavidad en la literatura.

Definición 1. (\(L\)-suavidad) Sea \(\Omega\subset\RR^p\) convexo y sea \(f:\RR^p\to\RR\) una función diferenciable. Se dice que \(f\) es \(L\)-suave si su gradiente es \(L\)-Lipschitz continuo, esto es, \[ \|\nabla f(\xx) - \nabla f(\yy)\|_{2} \leq L \|\xx - \yy\|_{2} \qquad \forall \xx, \yy \in \Omega. \]

Una consecuencia inmediata de la \(L\)-suavidad es que la función admite una cota superior cuadrática. Posteriormente, esta propiedad será extremadamente útil para cuantificar la mejora de un paso del algoritmo de descenso por gradiente, lo cual a menudo se denomina lema del descenso del gradiente.

Teorema 1. (Cota superior cuadrática) Sea \(\Omega\in\RR^p\) convexo y sea \(f: \RR^p \to \mathbb{R}\) una función \(L\)-suave. Se verifica \[ f(\yy) \leq f(\xx) + \langle \nabla f(\xx), \yy - \xx \rangle_2 + \frac{L}{2} \|\yy - \xx\|_{2}^{2} \quad \forall \xx, \yy \in \Omega. \]

Mostrar detalles

Demostración

Definamos la recta que conecta \(\xx\) con \(\yy\) como \(\gamma(t):=t\yy+(1-t)\xx\) y la restricción de \(f\) sobre dicha recta como \(h(t):=f(\gamma(t))\). El Teorema Fundamental del Cálculo permite escribir \[ h(1)-h(0)=\int_0^1h'(t)\, dt. \tag{1} \]

Pero \(h(1)=f(\yy)\), \(h(0)=f(\xx)\) y \[ h'(t)=\langle\nabla f(\gamma(t)),\gamma'(t)\rangle_2=\langle \nabla f(t\yy+(1-t)\xx), \yy-\xx \rangle_2. \]

Reemplazando en (1) resulta \[ \begin{align*} f(\yy)-f(\xx)&=\int_0^1\langle \nabla f(t\yy+(1-t)\xx), \yy-\xx\rangle_2\,dt\\ &=\langle\nabla f(\xx), \yy-\xx\rangle_2+\int_0^1\langle\nabla f(t\yy+(1-t)\xx)-\nabla f(\xx), \yy-\xx\rangle_2\,dt\\ &\leq \langle\nabla f(\xx), \yy-\xx\rangle_2+\int_0^1\|\nabla f(t\yy+(1-t)\xx)-\nabla f(\xx)\|_2\|\yy-\xx\|_2\,dt, \end{align*} \]

donde en el último paso se utilizó la desigualdad de Cauchy-Schwarz. Observar que el primer factor del integrando es el cambio de gradiente entre dos puntos, lo cual puede ser acotado en virtud de la \(L\)-suavidad; es decir \[ \|\nabla f(t\yy+(1-t)\xx)-\nabla f(\xx)\|_2\leq L\|t\yy+(1-t)\xx-\xx\|_2=tL\|\yy-\xx\|_2. \]

Finalmente nos queda \[ \begin{align*} f(\yy)-f(\xx)&\leq \langle\nabla f(\xx), \yy-\xx\rangle_2+ \int_0^1 tL\|\yy-\xx\|_2^2\,dt\\ &=\langle\nabla f(\xx), \yy-\xx\rangle_2+L\|\yy-\xx\|_2^2\int_0^1t\,dt.\\ &=\langle\nabla f(\xx), \yy-\xx\rangle_2+\frac{L}{2}\|\yy-\xx\|_2^2. \end{align*} \]

\(\blacksquare\)

Teorema 2. (Lema del descenso por gradiente) Sea \(f:\RR^p\to\RR\) una función \(L\)-suave. Para cualquier \(0 < \eta \leq \frac{1}{L}\), cada paso del método de descenso por gradiente garantiza

\[ f(\xx_{t+1}) \leq f(\xx_{t}) - \frac{\eta}{2} \|\nabla f(\xx_{t})\|_{2}^{2}. \]

Mostrar detalles

①

El Teorema 2 nos asegura que, para funciones \(L\)-suaves, existe una buena elección de la tasa de aprendizaje que permite garantizar que con cada paso del método de descenso por gradiente se mejorará el valor de la función, siempre que el punto actual no tenga un gradiente nulo.

Es importante remarcar que el resultado anterior no requiere que \(f\) sea convexa.

②

Si \(f\) está acotada inferiormente, el lema asegura que, eventualmente, algún gradiente será lo suficientemente pequeño. En efecto, para la \(T\)-ésima iteración, la aplicación sucesiva del lema resulta en \[ f(\xx_T)\leq f(\xx_0)-\frac{\eta}{2}\sum_{t=0}^{T-1}\|\nabla f(\xx_t)\|_2^2. \]

Por lo tanto, para el valor óptimo \(p^\star:=\inf\{f(\xx)\}\) debe ocurrir \[ \frac{1}{T}\sum_{t=0}^{T-1}\|\nabla f(\xx_t)\|_2^2\leq \frac{2}{\eta T}\left(f(\xx_0)-p^\star\right). \]

Esta última desigualdad nos asegura que existe \(0\leq \tilde{t}\leq T-1\) tal que \[ \|\nabla f(\xx_{\tilde{t}})\|_2^2\leq \frac{2}{\eta T}\left(f(\xx_0)-p^\star\right). \]

Observar que la cota obtenida depende del punto inicial \(\xx_0\). Cuanto más cercano esté a un punto óptimo, menor será el valor de la cota. Esto resalta la importancia de una buena elección del punto inicial para acelerar la convergencia del método.

Demostración

La cota superior cuadrática del Teorema 1 para \(\xx=\xx_t\) y \(\yy=\xx_{t+1}\) es \[ f(\xx_{t+1})\leq f(\xx_t)+\langle\nabla f(\xx_t),\xx_{t+1}-\xx_t\rangle_2+\frac{L}{2}\|\xx_{t+1}-\xx_t\|_2^2. \]

Utilizando en el lado derecho la fórmula de descenso por gradiente \(\xx_{t+1}=\xx_t-\eta\nabla f(\xx_t)\), se obtiene: \[ \begin{align*} f(\xx_{t+1})&\leq f(\xx_t)+\underbrace{\langle\nabla f(\xx_{t}), -\eta\nabla f(\xx_t)\rangle_2}_{-\eta\|\nabla f(\xx_t)\|_2^2}+\frac{L}{2}\eta^2\|\nabla f(\xx_t)\|_2^2\\[3pt] &=f(\xx_t)-\eta \left(1-\frac{L}{2}\eta\right)\|\nabla f(\xx_t)\|_2^2. \end{align*} \]

Cuando \(\eta\leq\frac{1}{L}\), el paréntesis es \(1-\frac{L}{2}\eta\geq\frac{1}{2}\). Realizando este cambio, se obtiene el resultado.

\(\blacksquare\)

Convergencia para funciones objetivos convexas

El Teorema 2 provee una tasa de convergencia para la norma del gradiente de la función objetivo, asegurándonos que al menos un punto en \(T\) iteraciones debe verificar \[ \|\nabla f(\xx_t)\|_2\leq\sqrt{2\frac{f(\xx_0-p^\star)}{\eta T}}. \]

Sin embargo, no proporciona ninguna garantía sobre la brecha \(f(\xx_t)-p^\star\). En otras palabras, un gradiente pequeño es necesario para acercarse al punto óptimo, pero no suficiente para asegurar que el valor de la función esté efectivamente cerca del valor óptimo.

Afortunadamente, cuando la función objetivo es convexa, sí es posible establecer una tasa de convergencia para el método de descenso por gradiente.

Lema 1. Sea \(f:\RR^p\to\RR\) una función diferenciable y convexa. Para cualquier elección del tamaño de paso \(\eta\), todo par de puntos consecutivos \((\xx_t,\xx_{t+1})\) del método de descenso por gradiente satisface \[ f(\xx_{t}) \leq f(\xx) + \frac{1}{2\eta} \left( \|\xx - \xx_{t}\|_{2}^{2} - \|\xx - \xx_{t+1}\|_{2}^{2} + \|\xx_{t+1} - \xx_{t}\|_{2}^{2} \right) \qquad \forall \xx \in \mathbb{R}^{p}. \]

Mostrar detalles

Demostración

Por convexidad de \(f\), para todo \(\xx\) se cumple \[ f(\xx_t)-f(\xx)\leq\langle \nabla f(\xx_t),\,\xx_t-\xx\rangle_2. \]

Usando la actualización \(\xx_{t+1}=\xx_t-\eta\,\nabla f(\xx_t)\), se tiene \[ \begin{align*} f(\xx_t)-f(\xx)&\leq\langle \frac{\xx_t-\xx_{t+1}}{\eta},\,\xx_t-\xx\rangle_2 \\ &=\frac{1}{\eta}\langle \xx_t-\xx_{t+1},\xx_t-\xx\rangle_2. \end{align*} \tag{2} \]

Aplicamos la identidad de tres puntos \[ 2\langle \uu-\vv,\,\uu-\ww\rangle_2=\|\uu-\vv\|_2^2+\|\uu-\ww\|_2^2-\|\vv-\ww\|_2^2, \] con \(\uu=\xx_t\), \(\vv=\xx_{t+1}\) y \(\ww=\xx\), para obtener \[ \langle \xx_t-\xx_{t+1},\xx_t-\xx\rangle_2 =\frac{1}{2}\left(\|\xx_t-\xx_{t+1}\|_ 2^2+\|\xx_t-\xx\|_2^2-\|\xx_{t+1}-\xx\|_2^2\right). \] Sustituyendo esto último en (2) y reordenando, se obtiene la cota enunciada.

Teorema 3. Sea \(f:\RR^p\to\RR\) una función \(L\)-suave y convexa con minimizador \(\xx^\star \in \RR^p\), y sea \(0 < \eta \leq \frac{1}{L}\). El método de descenso por gradiente verifica \[ f(\xx_{t}) - f(\xx^{*}) \leq \frac{\|\xx^\star - \xx_{0}\|_{2}^{2}}{2 t \eta} \qquad \forall t\in\NN. \]

Mostrar detalles

①

Aunque el método de descenso por gradiente garantiza que el valor de la función se acerque al óptimo, no siempre asegura que los puntos iterados converjan rápidamente al punto óptimo \(\xx^\star\). Para obtener garantías más fuertes sobre la rapidez con la que las iteraciones se acercan al punto óptimo, se requieren condiciones adicionales que permitan no solo que \(f(\xx_t)\to p^\star\) sino también que \(\|\xx_t-\xx^\star\|_2\) converja rápidamente (ver, por ejemplo, condición de Polyak-Łojasiewicz).

Demostración

Sean \((\xx_t,\xx_{t+1})\) dos puntos consecutivos de la iteración de descenso por gradiente. Entonces \[ \|\xx_{t+1}-\xx_{t}\|_2^2=\eta^2\|\nabla f(\xx_t)\|_2^2. \]

De esta igualdad y por Lema 1, tenemos que \[ f(\xx_{t}) \leq f(\xx) + \frac{1}{2\eta} \left( \|\xx - \xx_{t}\|_{2}^{2} - \|\xx - \xx_{t+1}\|_{2}^{2}\right)+\frac{\eta}{2}\|\nabla f(\xx_t)\|_2^2 \qquad \forall \xx \in \mathbb{R}^{p}. \]

Pero la \(L\)-suavidad de \(f\) nos permite usar el Teorema 2: para \(0\leq\eta\leq\frac{1}{L}\) se cumple \(\frac{\eta}{2}\|\nabla f(\xx_t)\|_2^2\leq f(\xx_t)-f(\xx_{t+1})\). Reemplazando en la expresión anterior, resulta \[ f(\xx_{t+1})\leq f(\xx)+ \frac{1}{2\eta} \left( \|\xx - \xx_{t}\|_{2}^{2} - \|\xx - \xx_{t+1}\|_{2}^{2}\right)\qquad\forall\xx\in\RR^p. \tag{3} \]

Sumando en ambos términos de (3) sobre \(t=0,1,\ldots,T-1\), con \(T\in\NN\) arbitrario, y teniendo en cuenta que el lado derecho es telescópico, obtenemos \[ \sum_{t=0}^{T-1}f(\xx_{t+1})\leq Tf(\xx)+\frac{1}{2\eta}\left(\|\xx-\xx_0\|_2^2-\|\xx-\xx_T\|_2^2\right)\qquad\forall\xx\in\RR^p. \]

Descartando el término \(\|\xx-\xx_T\|_2^2\), por estar restando, y aplicando esta desigualdad a \(\xx=\xx^\star\), se deduce que \[ \sum_{t=0}^{T-1}f(\xx_{t+1})\leq Tf(\xx^{\star})+\frac{1}{2\eta}\|\xx^{\star}-\xx_0\|_2^2. \]

Por último, vamos a usar el hecho que \(Tf(\xx_T)\leq\sum_{t=0}^{T-1}f(\xx_{t+1})\); esto es cierto ya que el Teorema 2 asegura que \(\{f(\xx_t) \mid t\in\NN\}\) es no creciente. Finalmente \[ \begin{align*} Tf(\xx_T)&\leq T f(\xx^\star)+\frac{1}{2\eta}\|\xx^{\star}-\xx_0\|_2^2\\ f(\xx_T)-f(\xx^{\star})&\leq \frac{1}{2T\eta}\|\xx^{\star}-\xx_0\|_2^2. \end{align*} \]

\(\blacksquare\)

Método de descenso por gradiente proyectado

Vamos a ver ahora como adaptar el método de descenso por gradiente a problemas de optimización con restricciones de la forma \[ \begin{array}{ll} \text{minimizar } & f(\xx)\\ \text{sujeto a } & \xx\in\Omega. \end{array} \]

En este caso, supondremos que \(f\) es diferenciable y que el conjunto factible \(\Omega\) es cerrado y convexo. La forma natural de extender el método de descenso por gradiente consiste en proyectar los puntos obtenidos sobre \(\Omega\), de manera tal de asegurarnos que la sucesión \(\{\xx_t\mid t\in\mathbb{N}_0\}\subset\Omega\).

Importante

La proyección ortogonal de un punto \(\yy\in \RR^p\) sobre un conjunto \(\Omega\) se define como

\[ \Pi_{\Omega}(\yy) := \arg\min_{\xx \in \Omega} \|\xx - \yy\|_2. \]

Cuando \(\Omega\) es cerrado y convexo, la proyección ortogonal existe y es única. Además, para todo \(\xx\in\Omega\) y \(\yy\in\RR^p\), se verifican las siguientes propiedades:

1. \((\xx-\Pi_\Omega(\yy))^\top(\yy-\Pi_\Omega(\yy))\leq 0.\)

2. \(\|\xx-\Pi_\Omega(\yy)\|_2^2+\|\yy-\Pi_\Omega(\yy)\|_2^2\leq\|\xx-\yy\|_2^2.\)

Método de descenso por gradiente proyectado

---

Dado un punto inicial \(\xx_0\in\Omega\) y una tasa de aprendizaje \(\eta > 0\):

repetir para \(t = 0,1,2,\dots\):

1° Calcular dirección \(-\nabla f(\xx_t)\).

2° Calcular paso de gradiente \(\yy_{t+1} := \xx_t - \eta \nabla f(\xx_t)\).

3° Proyectar sobre \(\Omega\): \(\xx_{t+1} := \Pi_{\Omega}(\yy_{t+1})\).

hasta que se satisfaga el criterio de parada.

---

Figura 2. Interpretación geométrica del método de descenso por gradiente proyectado.

Vamos a implementar en Python este método. Cabe destacar que el paso de proyección es por sí mismo un problema de optimización, cuyo objetivo es hallar el punto más cercano dentro del conjunto factible \(\Omega\). En algunos casos, como por ejemplo \(\Omega=[0,1]^n\), el conjunto factible tiene una forma especial que permite resolver la proyección de forma explícita y eficiente.

Por lo tanto, en relación al método de descenso por gradiente, se agrega un nuevo argumento:

• proy: función de proyección sobre el conjunto factible.

import numpy as np

def projected_gradient_descent(f, grad_f, x_inicial, proy,
                               lr=0.1, max_iter=100,
                               tol_grad=None, tol_x=None,
                               verbose=True):
  
    x = np.array(x_inicial, dtype=float)
    x_iter = [x.copy()]
    f_iter = [f(x)]

    for t in range(1, max_iter + 1):
      
      grad = grad_f(x)

      # Criterio de parada por norma del gradiente:
      if tol_grad is not None and np.linalg.norm(grad) < tol_grad:
        if verbose:
          print(f"Parada en iteración {t}: |grad_f| < {tol_grad}")
        t = t-1
        break

      y = x - lr * grad
      x_new = proy(y)

      # Criterio de parada por norma de diferencia entre iteraciones:
      if tol_x is not None and np.linalg.norm(x_new - x) < tol_x:
        if verbose:
          print(f"Parada en iteración {t}: |x_t - x_(t+1)| < {tol_x}")
        x = x_new
        x_iter.append(x.copy())
        f_iter.append(f(x))
        break

      x = x_new
      x_iter.append(x.copy())
      f_iter.append(f(x))

    if verbose:
      print(f"Iteración final: {t}")
      print(f"Último punto: {x}")
      print(f"Valor de f: {f(x)}")

    return x_iter, f_iter

Ejemplo 2 Vamos a utilizar el método de descenso por gradiente proyectado para resolver el problema \[ \begin{array}{ll} \text{minimizar } & 2(x-2)^2+5(y-3)^2\\ \text{sujeto a } & \xx\in\Omega=[0,1]\times [0,1]. \end{array} \]

En este caso la función de proyección es sencilla: consiste en recortar cada coordenada al intervalo correspondiente; es decir \[ \Pi_{[0,1]\times[0,1]}(x,y):=\begin{pmatrix} \min(\max(x,0),1) \\ \min(\max(y,0),1) \end{pmatrix}. \]

Esto se calcula rápidamente con la función np.clip de NumPy.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Función y gradiente:
def f(x):
    return 2*(x[0] - 2)**2 + 5*(x[1] - 3)**2

def grad_f(x):
    return np.array([4 * (x[0] - 2), 10 * (x[1] - 3)])

# Proyección:
def proy(x):
    return np.clip(x, 0, 1)

# Parámetros:
x_inicial = (0, 0)
lr = 0.01             
max_iter = 20
tol_grad = 1e-3
tol_x = 1e-3

# Ejecutar PGD:
x_iter, f_iter = projected_gradient_descent(f, grad_f, x_inicial, proy, lr, max_iter, tol_grad, tol_x)

Parada en iteración 18: |x_t - x_(t+1)| < 0.001
Iteración final: 18
Último punto: [1. 1.]
Valor de f: 22.0

La secuencia de valores obtenidas es:

x_arr = np.array(x_iter)
x_vals = x_arr[:, 0]
y_vals = x_arr[:, 1]
tabla = pd.DataFrame({'x': x_vals, 'y': y_vals})
print(tabla)

           x      y
0   0.000000  0.000
1   0.080000  0.300
2   0.156800  0.570
3   0.230528  0.813
4   0.301307  1.000
5   0.369255  1.000
6   0.434484  1.000
7   0.497105  1.000
8   0.557221  1.000
9   0.614932  1.000
10  0.670335  1.000
11  0.723521  1.000
12  0.774580  1.000
13  0.823597  1.000
14  0.870653  1.000
15  0.915827  1.000
16  0.959194  1.000
17  1.000000  1.000
18  1.000000  1.000

Por último, vamos a realizar la gráfica en el dominio \(\RR^2\) de la función.

# Grilla para graficar:
x = np.linspace(-0.5, 1.5, 100)
y = np.linspace(-0.5, 1.5, 100)
X, Y = np.meshgrid(x, y)
Z = f(np.array([X, Y]))

# 📈:
plt.figure(figsize=(10, 6))

# Curvas de nivel:
contours = plt.contour(X, Y, Z, levels=10, cmap='viridis')
plt.clabel(contours, inline=True, fontsize=8)

# Ruta de descenso por gradiente proyectado:
plt.plot(x_vals, y_vals, marker='o', linestyle='--', color='red', label='Iteraciones')
plt.scatter(2, 3, color='blue', label='Mínimo sin restricciones', zorder=5)

# Caja [0,1]^2 en azul:
caja_x = [0, 1, 1, 0, 0]
caja_y = [0, 0, 1, 1, 0]
plt.plot(caja_x, caja_y, color='blue', linewidth=2, linestyle='-', label='$\Omega = [0,1]^2$')

plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='upper right', facecolor='white', framealpha=1)
plt.grid(True)
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1.5)
plt.show()

<>:21: SyntaxWarning: invalid escape sequence '\O'
<>:21: SyntaxWarning: invalid escape sequence '\O'
C:\Users\isaia\AppData\Local\Temp\ipykernel_14328\4178567754.py:21: SyntaxWarning: invalid escape sequence '\O'
  plt.plot(caja_x, caja_y, color='blue', linewidth=2, linestyle='-', label='$\Omega = [0,1]^2$')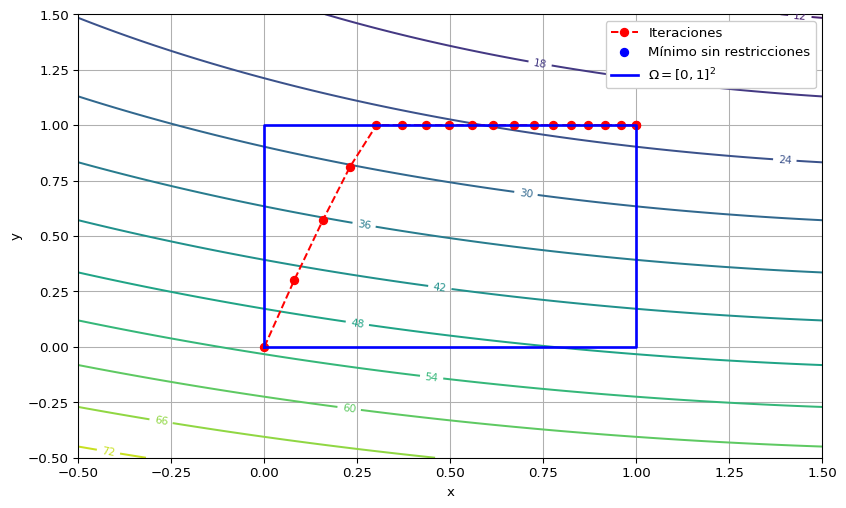

Resultados de convergencia

Bajo condiciones similares a las del método sin restricciones, el método proyectado también garantiza convergencia del valor de la función objetivo.

Teorema 4. (Lema del descenso por gradiente proyectado) Sea \(f:\RR^p\to\RR\) una función \(L\)-suave. Entonces, para cualquier \(0 < \eta \leq \frac{1}{L}\), cada paso del método de descenso por gradiente proyectado garantiza

\[ f(\xx_{t+1}) \leq f(\xx_{t}) - \frac{\eta}{2} \|\nabla f(\xx_{t})\|_{2}^{2}+\frac{1}{2\eta}\|\yy_{t+1}-\xx_{t+1}\|_2^2. \]

Mostrar detalles

Demostración

Como en la demostración del Teorema 2, partimos de la cota superior cuadrática del Teorema 1 para \(\xx=\xx_t\) y \(\yy=\xx_{t+1}\): \[ f(\xx_{t+1})\leq f(\xx_t)+\langle\nabla f(\xx_t), \xx_{t+1}-\xx_t\rangle_2+\frac{L}{2}\|\xx_{t+1}-\xx_t\|_2^2. \]

En este caso, debemos utilizar la fórmula \(\yy_{t+1}:=\xx_t-\eta\nabla f(\xx_t)\) para sustituir \(\nabla f(\xx_t)\) en el segundo término de la suma, obteniendo

\[ f(\xx_{t+1})\leq f(\xx_t)-\frac{1}{\eta}\langle\yy_{t+1}-\xx_t,\xx_{t+1}-\xx_t\rangle_2+\frac{L}{2}\|\xx_{t+1}-\xx_t\|_2^2. \]

Ahora, expresaremos \(\langle\yy_{t+1}-\xx_t,\xx_{t+1}-\xx_t\rangle_2\) mediante la identidad \(\uu\cdot\vv=\frac{1}{2}\left(\|\uu\|_2^2+\|\vv\|_2^2-\|\uu-\vv\|_2^2\right)\). Además, para el último término usaremos la hipótesis \(L\leq \frac{1}{\eta}\). Resulta \[ \begin{align*} f(\xx_{t+1})&\leq f(\xx_t)-\frac{1}{2\eta}\left(\|\yy_{t+1}-\xx_t\|_2^2+\|\xx_{t+1}-\xx_t\|_2^2-\|\yy_{t+1}-\xx_{t+1}\|_2^2\right)+\frac{1}{2\eta}\|\xx_{t+1}-\xx_t\|_2^2\\ &=f(\xx_t)-\frac{1}{2\eta}\left(\|\underbrace{\yy_{t+1}-\xx_t}_{-\eta\nabla f(\xx_t)}\|_2^2-\|\yy_{t+1}-\xx_{t+1}\|_2^2\right)\\[3pt] &\leq f(\xx_t)-\frac{1}{2\eta}\left(\eta^2\|\nabla f(\xx_t)\|_2^2-\|\yy_{t+1}-\xx_{t+1}\|_2^2\right)\\ &=f(\xx_t)-\frac{\eta}{2}\|\nabla f(\xx_t)\|_2^2+\frac{1}{2\eta}\|\yy_{t+1}-\xx_{t+1}\|_2^2. \end{align*} \]

\(\blacksquare\)

A pesar de que en este Teorema, en relación con el lema del descenso por gradiente (Teorema 2), aparece el término adicional \(\frac{1}{2\eta}\|\yy_{t+1}-\xx_{t+1}\|_2^2\), este puede ser cancelado utilizando las propiedades de proyección ortogonal en \(\Omega\) cerrado y convexo. En consecuencia, se obtiene para el método de descenso por gradiente proyectado el mismo resultado de convergencia del Teorema 3 para el método de descenso por gradiente.

Teorema 5. Sea \(f:\RR^p\to\RR\) una función convexa y \(L\)-suave, con minimizador \(\xx^\star\in\Omega\), donde \(\Omega\subset\RR^p\) es un conjunto cerrado y convexo, y sea \(0<\eta\leq\frac{1}{L}\). El método de descenso por gradiente proyectado verifica

\[ f(\xx_t) - f(\xx^\star) \leq \frac{\|\xx_0 - \xx^\star\|_2^2}{2t\eta}, \qquad \forall t\in\NN. \]

📝

Escriba la demostración del Teorema 5, siguiendo el razonamiento usado para el Teorema 3.

Método de descenso por gradiente estocástico

Presentaremos una variante del descenso por gradiente que resulta particularmente útil cuando la función objetivo se expresa como una suma de muchas funciones, es decir,

\[ f(\xx) = \frac{1}{n} \sum_{i=1}^{n} f_i(\xx). \]

Esto sucede habitualmente en problemas de aprendizaje supervisado, donde la función a optimizar es un costo que puede definirse como suma de los costos individuales de cada dato.

El método de descenso por gradiente requiere calcular el gradiente completo \(\nabla f(\xx)\) en cada paso. En cambio, la versión estocástica reemplaza ese gradiente por una estimación basada en una muestra, lo cual reduce drásticamente el costo computacional por iteración. Esto lo vuelve especialmente atractivo en contextos con grandes volúmenes de datos (big data), donde calcular el gradiente total puede ser inviable.

Método de descenso por gradiente estocástico

---

Dado un punto inicial \(\xx_0\) y una tasa de aprendizaje \(\eta>0\):

repetir para \(t = 0,1,2,\dots\):

1° Elegir un índice \(i\) al azar de \(\{1,\dots,n\}\).

2° Calcular el gradiente estocástico \(\nabla f_i(\xx_t)\).

3° Actualizar \(\xx_{t+1} := \xx_t - \eta \nabla f_i(\xx_t)\).

hasta que se satisfaga un criterio de parada.

---

Importante

Otra variante ampliamente utilizada en la práctica es el descenso por gradiente mini-batch, donde en lugar de usar un único índice \(i_t\), se toma un subconjunto aleatorio (mini-batch) de índices para estimar el gradiente mediante el promedio de los gradientes evaluados en ese lote. Es decir, el 2° paso del algoritmo anterior adopta la forma

\[ \frac{1}{\#(B_t)}\sum_{i\in B_t}\nabla f_i(\xx_t), \]

donde \(\#(B_t)\) denota el tamaño del mini-batch.

Esto permite un equilibrio entre la alta varianza del método estocástico y el alto costo computacional del método de descenso por gradiente completo. Además, el uso de mini-batches es especialmente adecuado para estrategias computacionales tales como la programación paralela.

Métodos de segundo orden

Vamos a iniciar el estudio de los métodos de segundo orden, que además del gradiente utilizan también la Hessiana (la segunda derivada) de la función objetivo.

Método de Newton

Para el caso sin restricciones

\[ \begin{array}{ll} \text{minimizar } & f(\xx), \end{array} \]

asumimos que \(f\) es una función dos veces diferenciable. En este caso, podemos analizar qué sucede si, en lugar de la aproximación de Taylor de primer orden, usamos la expansión de segundo orden alrededor de un punto \(\xx_t\):

\[f(\xx)\approx \underbrace{f(\xx_t)+\nabla f(\xx_t)^\top(\xx-\xx_t)+\frac{1}{2}(\xx-\xx_t)^\top \nabla^2 f(\xx_t)(\xx-\xx_t)}_{q_t(\xx)},\]

donde \(\nabla^2 f(\xx_t)\) es la matriz Hessiana de \(f\) en \(\xx_t\). Teniendo en cuenta que la aproximación \(q_t\) es una función de \(\xx\), al analizar \(\nabla q_t(\xx)=\mathbf{0}\) se obtiene inmediatamente la ecuación \[ \nabla f(\xx_t)+\nabla^2 f(\xx_t)(\xx-\xx_t)=\mathbf{0}, \]

lo cual deriva en la siguiente fórmula iterativa:

\[ \xx_{t+1}:=\xx_t-\left[\nabla^2f(\xx_t)\right]^{-1}\nabla f(\xx_t). \]

Comparando esta fórmula con la actualización del método de descenso por gradiente, vemos que ahora la dirección de descenso cambia a \(-\left[\nabla^2f(\xx_t)\right]^{-1}\nabla f(\xx_t)\), lo cual requiere la suposición de que la matriz Hessiana \(\nabla^2 f(\xx_t)\) sea invertible. En caso de no serlo, la forma alternativa es resolver el sistema de ecuaciones \[ \nabla^2 f(\xx_t)(\xx_{t+1}-\xx_t)=-\nabla f(\xx_t). \]

Figura 3. Interpretación geométrica del método de Newton-Raphson para aproximar una solución de \(f'(x)=0\).

Método de Newton-Raphson para una variable

\[ x_{t+1}:=x_t-\frac{f'(x_t)}{f''(x_t)}. \]

El cambio de \(-\nabla f(\xx_t)\) (dirección del método de descenso por gradiente) por \(-\left[\nabla^2f(\xx_t)\right]^{-1}\nabla f(\xx_t)\) se conoce como precondicionamiento del gradiente por la matriz Hessiana. Esto permite definir la generalización natural del método de descenso por gradiente al contexto de segundo orden.

Método de Newton

---

Dado un punto inicial \(\xx_0 \in \mathrm{dom}\, f\):

repetir para \(t=0,1,2,\dots\):

1° Calcular el gradiente \(\nabla f(\xx_t)\) y la matriz Hessiana \(\nabla^2 f(\xx_t)\).

2° Actualizar \(\xx_{t+1} := \xx_t-\left[\nabla^2 f(\xx_t)\right]^{-1}\nabla f(\xx_t)\), o bien resolver el sistema de ecuaciones \(\nabla^2f(\xx_t)(\xx_{t+1}-\xx_t)=-\nabla f(\xx_t)\).

hasta que se cumpla un criterio de parada.

---

Importante

Una variante es el método de Newton con paso reducido, donde se introduce la tasa de aprendizaje \(0<\eta\leq 1\). Esta se utiliza en en la práctica para controlar la magnitud de las actualizaciones y hacer el método más estable.La actualización queda dada por \[ \xx_{t+1} := \xx_t-\eta \left[\nabla^2 f(\xx_t)\right]^{-1}\nabla f(\xx_t) \]

La implementación en Python requiere el siguiente argumento adicional:

• hess_f: función Hessiana de \(f\).

def newton_method(f, grad_f, hess_f, x_inicial, lr=0.1,         
                  max_iter=100, tol_grad=None, tol_x=None, verbose=True):
    
    x = np.array(x_inicial, dtype=float)
    x_iter = [x.copy()]
    f_iter = [f(x)]

    for t in range(1, max_iter + 1):
      grad = grad_f(x)
      hess = hess_f(x)

      # Criterio de parada por norma del gradiente:
      if tol_grad is not None and np.linalg.norm(grad) < tol_grad:
        if verbose:
          print(f"Parada en iteración {t}: |grad_f| < {tol_grad}")
        t = t-1
        break

      try:
        p = -np.linalg.solve(hess, grad) 
      except np.linalg.LinAlgError:
        if verbose:
          print(f"Hessiana no invertible en iteración {t}")
        break

      x_new = x + lr * p

      # Criterio de parada por norma de diferencia entre iteraciones:
      if tol_x is not None and np.linalg.norm(x_new - x) < tol_x:
        if verbose:
          print(f"Parada en iteración {t}: |x_t - x_(t+1)| < {tol_x}")
        x = x_new
        x_iter.append(x.copy())
        f_iter.append(f(x))
        break

      x = x_new
      x_iter.append(x.copy())
      f_iter.append(f(x))

    if verbose:
      print(f"Iteración final: {t}")
      print(f"Último punto: {x}")
      print(f"Valor de f: {f(x)}")

    return x_iter, f_iter

Ejemplo 3 Vamos a utilizar el método de Newton para aproximarnos al valor mínimo de

\[ f(x,y)=2(x-2)^2+5(y-3)^2, \]

para poder comparar con el Ejemplo 1. La Hessiana es

\[ \nabla^2 f(x,y) = \begin{pmatrix} 4&0\\0&10 \end{pmatrix}. \]

En primer lugar, utilizaremos la variante con paso reducido, con \(\eta=0.05\).

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Función y gradiente:
def f(x):
    return 2*(x[0] - 2)**2 + 5*(x[1] - 3)**2

def grad_f(x):
    return np.array([4 * (x[0] - 2), 10 * (x[1] - 3)])

def hess_f(x):
    return np.array([[4, 0], [0, 10]]) 

# Parámetros:
x_inicial = (0, 0)
lr = 0.05               
max_iter = 100
tol_grad = 1e-3
tol_x = 1e-3

# Ejecutar Newton:
x_iter, f_iter = newton_method(f, grad_f, hess_f, x_inicial, lr, max_iter, tol_grad, tol_x)

Iteración final: 100
Último punto: [1.98815894 2.98223841]
Valor de f: 0.0018577913111879544

La secuencia de valores obtenidas es:

x_arr = np.array(x_iter)
x_vals = x_arr[:, 0]
y_vals = x_arr[:, 1]
tabla = pd.DataFrame({'x': x_vals, 'y': y_vals})
print(tabla)

            x         y
0    0.000000  0.000000
1    0.100000  0.150000
2    0.195000  0.292500
3    0.285250  0.427875
4    0.370988  0.556481
..        ...       ...
96   1.985462  2.978193
97   1.986189  2.979284
98   1.986880  2.980320
99   1.987536  2.981304
100  1.988159  2.982238

[101 rows x 2 columns]

Por último, vamos a realizar la gráfica en el dominio \(\RR^2\) de la función.

# Grilla para graficar:
x = np.linspace(-0.5, 7, 100)
y = np.linspace(-0.5, 5, 100)
X, Y = np.meshgrid(x, y)
def f_xy(x, y):
    return f(np.array([x, y]))
Z = f_xy(X, Y)


# 📈:
plt.figure(figsize=(10, 6))

# Curvas de nivel:
contours = plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.clabel(contours, inline=True, fontsize=8)

# Ruta de descenso por gradiente:
plt.plot(x_vals, y_vals, marker='o', linestyle='--', color='red', label='Iteraciones')
plt.scatter(2, 3, color='blue', label='Mínimo', zorder=5)

plt.xlabel('x')
plt.ylabel('y')
plt.xlim(-0.2, 4)
plt.ylim(-0.2, 5)
plt.legend(loc='upper right', facecolor='white', framealpha=1)
plt.grid(True)
plt.show()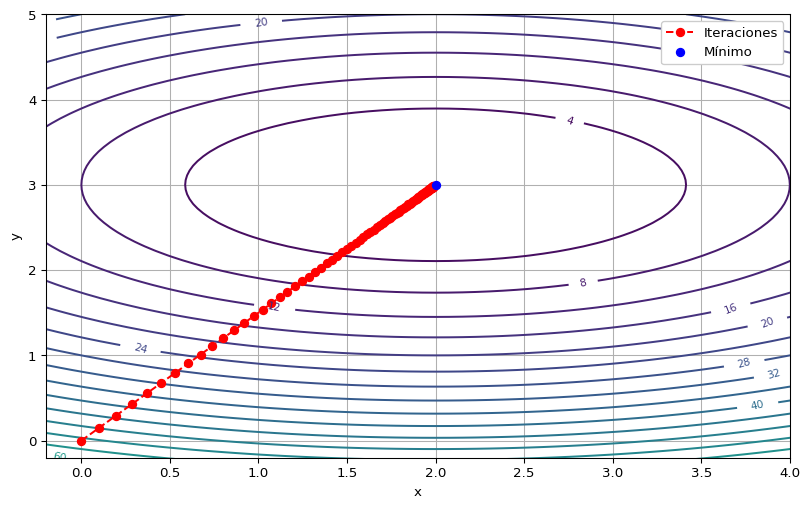

Observar que los puntos iterados son colineales. Esto ocurre en problemas cuadráticos, debido a que la matriz Hessiana es constante. Veamos qué pasa si aplicamos directamente el método de Newton clásico (\(\eta=1\)).

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Función y gradiente:
def f(x):
    return 2*(x[0] - 2)**2 + 5*(x[1] - 3)**2

def grad_f(x):
    return np.array([4 * (x[0] - 2), 10 * (x[1] - 3)])

def hess_f(x):
    return np.array([[4, 0], [0, 10]]) 

# Parámetros:
x_inicial = (0, 0)
lr = 1            
max_iter = 100
tol_grad = 1e-3
tol_x = 1e-3

# Ejecutar Newton:
x_iter, f_iter = newton_method(f, grad_f, hess_f, x_inicial, lr, max_iter, tol_grad, tol_x)

Parada en iteración 2: |grad_f| < 0.001
Iteración final: 1
Último punto: [2. 3.]
Valor de f: 0.0

x_arr = np.array(x_iter)
x_vals = x_arr[:, 0]
y_vals = x_arr[:, 1]
tabla = pd.DataFrame({'x': x_vals, 'y': y_vals})
print(tabla)

     x    y
0  0.0  0.0
1  2.0  3.0

En el ejemplo anterior, Newton clásico converge en una sola iteración debido a que la función es cuadrática, convexa y su Hessiana es constante y definida positiva, lo cual ilustra un escenario ideal. En general, para funciones más complejas, no solo el método de Newton puede requerir varias iteraciones, sino que además la convergencia depende fuertemente del punto inicial. A continuación, veremos condiciones que garantizan la convergencia local del método.

Garantías de convergencia local

En los métodos de optimización, las nociones de convergencia pueden referirse tanto a la sucesión \(\{f(\xx_t)\}\) de valores de la función objetivo como a la sucesión de puntos iterados \(\{\xx_t\}\). En el caso de los métodos basados en gradiente, los resultados vistos son de la forma \[ f(\xx_t)-f(\xx^\star)\leq \varepsilon(t). \]

Así, se garantiza que, bajo ciertas hipótesis globales, los valores de \(f(\xx_t)\) disminuyen hacia el valor óptimo \(p^\star:=f(\xx^\star)\), incluso si el punto inicial \(\xx_0\) está lejos de \(\xx^\star\).

En contraste, el método de Newton ofrece resultados de otra naturaleza: cuando ciertas suposiciones sobre la matriz Hessiana son ciertas, se verifica \(\xx_t\to\xx_\star\), donde \(\xx_\star\) es un punto crítico que puede ser un mínimo local. En consecuencia, esto representa un resultado de convergencia local, pues para que nos permita hallar el punto óptimo \(\xx^\star\), debemos asegurarnos de que el punto inicial \(\xx_0\) esté en una vecindad adecuada de él.No obstante, la ventaja respecto a los métodos basados en gradiente radica en que, si estamos lo suficientemente cerca del punto óptimo \(\xx^\star\), el método de Newton converge de manera extremadamente eficiente.

En primer lugar, enunciamos el siguiente teorema de convergencia.

Teorema 6. Sea \(f:\RR^p\to\RR\) una función dos veces diferenciable y sea \(\xx_\star\) un punto crítico. Supongamos que existe una bola \(B(\xx_\star,\varepsilon)\subset \text{dom}\,f\) tal que:

1. Existe \(\alpha>0\) tal que \[ \|\nabla^2f(\xx)^{-1}\|_2\leq\frac{1}{\alpha}\qquad\forall\xx\in B(\xx_{\star},\varepsilon). \]

2. Existe \(M\geq 0\) tal que \[ \|\nabla^2f(\xx)-\nabla^2f(\yy)\|_2\leq M\|\xx-\yy\|_2\qquad\forall\xx,\yy\in B(\xx_\star,\varepsilon) \]

Entonces, para \(\xx_t\in B(\xx_\star,\varepsilon)\) y \(\xx_{t+1}\) resultante del método de Newton, se verifica \[ \|\xx_{t+1}-\xx_\star\|_2\leq \frac{M}{2\alpha}\|\xx_t-\xx_{\star}\|_2^2. \]

Para concluir la idea de la rapidez de convergencia, el siguiente resultado establece la condición de cercanía de \(\xx_0\) respecto al punto crítico \(\xx_\star\). Por supuesto, como caso particular, también aplica a nuestro real interés de hallar \(\xx^\star\), siempre que se cumplan las condiciones.

Corolario 1. Bajo las condiciones del Teorema 6, si además \[ \|\xx_0-\xx_\star\|_2\leq \frac{\alpha}{M}, \] el método de Newton verifica \[ \|\xx_T-\xx_\star\|_2\leq\frac{\alpha}{M}\left(\frac{1}{2}\right)^{2^T-1}\qquad\forall T\geq 0. \]

Mostrar detalles

Demostración

Sin pérdida de generalidad, supongamos \(T>2\). El resultado se deriva de aplicar sucesivamente el Teorema 6: \[ \begin{align*} \|\xx_{T}-\xx_{\star}\|_2&\leq\frac{M}{2\alpha}\|\xx_{T-1}-\xx_\star\|_2^2\\ &\leq\frac{M}{2\alpha} \frac{M^2}{2^2\alpha^2}\|\xx_{T-2}-\xx_\star\|_2^4\\ &\;\vdots\\ &\leq \left(\frac{M}{2\alpha}\right)^{2^T-1}\|\xx_0-\xx_\star\|_2^{2^T} \\ &\leq \left(\frac{M}{2\alpha}\right)^{2^T-1}\left(\frac{\alpha}{M}\right)^{2^T}\\ &=\frac{\alpha}{M}\left(\frac{1}{2}\right)^{2^T-1}. \end{align*} \]

\(\blacksquare\)

Métodos Quasi-Newton

Si bien el método de Newton es muy atractivo por su rápida convergencia, presenta un alto costo computacional: en cada iteración es necesario o bien calcular e invertir la matriz Hessiana, o bien resolver el sistema de ecuaciones \[ \nabla^2f(\xx_t)(\xx_{t+1}-\xx_t)=-\nabla f(\xx_t). \]

Una alternativa natural surge a partir del método de la secante de una variable: en lugar de calcular la derivada exacta, se la aproxima a partir de la diferencia finita entre dos puntos.

Figura 4. Interpretación geométrica del método de la secante de una variable para aproximar una solución de \(f'(x)=0\).

Método de la secante de una variable

\[ x_{t+1}:=x_t-\frac{x_t-x_{t-1}}{f'(x_t)-f'(x_{t-1})}f'(x_t). \]

En el contexto multidimensional, la idea del método de la secante conduce a los métodos de Quasi-Newton: en lugar de usar la Hessiana exacta, se construye en cada paso una aproximación utilizando la información contenida en los gradientes.

Si \(H_t\in\SS^p\) satisface la condición de la secante \[ \nabla f(\xx_t)-\nabla f(\xx_{t-1})=H_t(\xx_t-\xx_{t-1}), \tag{4} \]

entonces el método de la secante consiste en actualizar \[ \xx_{t+1}:=\xx_t-H_t^{-1}\nabla f(\xx_t). \]

Importante

Si \(f:\RR^p\to\RR\) es dos veces diferenciable, la aproximación de Taylor de primer orden de \(\nabla f\) en \(\xx_t\) permite escribir \[ \nabla f(\xx_t)\approx\nabla f(\xx_{t-1})+\nabla^2f(\xx_{t-1})(\xx_t-\xx_{t-1}). \]

Por lo tanto, \[ \nabla f(\xx_t)-\nabla f(\xx_{t-1})=H_t(\xx_t-\xx_{t-1})\approx\nabla^2f(\xx_t)(\xx_t-\xx_{t-1}). \]

Podemos entonces esperar que \(H_t\approx\nabla^2f(\xx_t)\), lo cual significa que el método de la secante aproxima al método de Newton.

A diferencia de \(p=1\), donde \(H_t\) es único, para \(p>1\) la condición de la secante (4) tiene infinitas soluciones simétricas, puesto que determina un sistema de \(p\) ecuaciones con \(p(p+1)/2>p\) incógnitas (esto último, por ser \(H_t\) simétrica). En consecuencia:

Cualquier procedimiento que, en cada paso del método de la secante, elija una matriz simétrica \(H_t\) que cumpla la condición de la secante (4), da lugar a un algoritmo denominado método de Quasi-Newton.

Entre los métodos Quasi-Newton más utilizados se encuentran BFGS y su versión limitada en memoria L-BFGS, así como DFP y SR1. Todos ellos consisten en reglas específicas para actualizar la matriz \(H_t\), ofreciendo aproximaciones eficientes a la Hessiana sin necesidad de calcularla explícitamente.

Los métodos de Quasi-Newton logran un compromiso: mantienen la buena tasa de convergencia de Newton, pero evitando el costo de calcular y almacenar la Hessiana, lo que los hace especialmente útiles en problemas de gran escala.

Breve reseña de otros métodos

Más allá de los métodos analizados en esta sección, existen varias familias de algoritmos importantes que conviene mencionar:

• Métodos de segundo orden para problemas con restricciones: extensiones de Newton que incorporan restricciones sobre el dominio, como el Newton proyectado o los métodos de barrera. Permiten manejar problemas restringidos de manera directa, aunque requieren un análisis más sofisticado.

• Métodos de región de confianza: en lugar de aplicar un paso fijo, construyen un modelo cuadrático local de la función y limitan la actualización a una vecindad donde el modelo es fiable. Esto los hace más robustos que Newton clásico, incluso cuando la Hessiana no es definida positiva.

• Métodos de punto interior: se usan sobre todo para problemas con restricciones de desigualdad. Transforman el problema en una sucesión de problemas suavizados mediante funciones de barrera, permitiendo aproximarse al óptimo de forma estable.

• Otros enfoques modernos: incluyen el descenso por coordenadas, el método de Frank-Wolfe, algoritmos acelerados, y métodos adaptativos o sin gradiente, que son útiles para problemas de alta dimensión o funciones no diferenciables.

Actividades

💻 Prácticas

---

Referencias

Farina, G. Apuntes del curso MIT 6.7220: Nonlinear Optimization. Lecciones 12, 14 y 15 (2025) y Lección 12 (2024). Disponible en la página del curso.

Flammarion, N. Apuntes del curso EPFL CS-439: Optimization for machine learning, Lecciones 2, 3, 5 y 7. Disponible en este repositorio GitHub.